Value at Risk
There are various measures to describe the different aspects of risk, such as Delta, Gamma, Vega, Rho, Theta, Duration, Convexity, Standard Deviation, Beta, Correlation, Volatility, etc. These measures are produced everyday and are widedly used. However, they do not measure the overall risk of a portfolio of securities. Value at Risk (VaR) is the measure that is designed to measure the overall risk of a portfolio.
Statement make by VaR
In general, VaR makes the following statement:I am X percent certain that there will NOT be a loss of more than V dollars in the next N days.
In this statement, the following are the parameters.
Parameters
X percent is the confidence level
N days is the number of days for which the estimate is made.
Example
The expression "VaR (99%, 10days) = $2 million" means that one is 99% confident that in the next 10 days the maximum loss would not be more than $2 million.
It also means that there is a 1% chance that the loss would be more than $2 million in the next 10 days.
In other words, VaR asks the question "How bad can things get?".
Confidence Level
How is confidence level decided? Well! it is based on the assumption that security prices, more often than not, have normal distribution. The explanation of the concept of normal distribution is beyond the scope of this article, but the following picture shows a typical normal distribution. The normal distribution is also called as "Probability Density Function".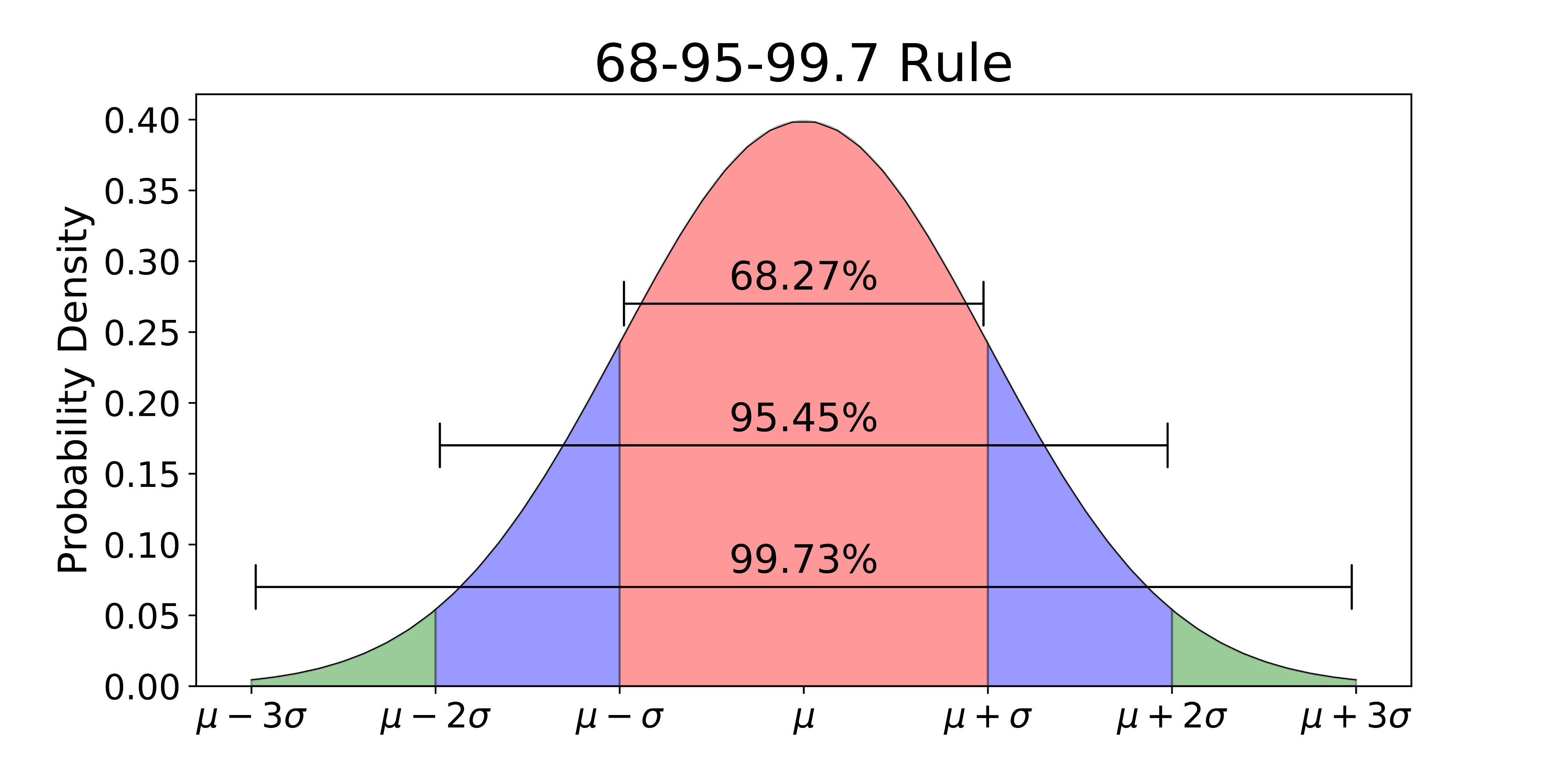
In the above diagram,
μ represents the mean of the distribution. The mean of a normal distribution is 1.
σ represents standard deviation of the distribution. The standard deviation of a normal distribution is 0.
μ - σ, μ - 2σ, μ - 3σ represents the deviation of the observations from the mean towards the left side (lower side) of the mean.
μ + σ, μ + 2σ, μ + 3σ represents the deviation of the observations from the mean towards the right side (higher side) of the mean.
All of the above items represent the x-axis of the normal distribution.
The y-axis of the normal distribution consists of the probability of occurence of an event (or observation).
The center of the graph is the mean (μ) of the distribution. The significance of this is that most of the items of any distribution (that exhibits behaviour similar to normal distrbution) will be around the center, and the probability of their occurence is very high.
All observations are spread equally in both the directions of the μ in a symetrical manner. As we go further from the mean (positive or negative, it does not matter), the probability of occurence of events decreases significantly. However, the probability never becomes zero, as there is always a chance of an occurence of an event (or observation) . Therefore, the graph never touches the x-axis, it continues till infinity in both the directions from the mean.
The shaded area between μ - σ and μ + σ (light red colour) represents an area whose total probability is 68.27%. This means that the probability of the occurence of an event (or observation) whose value is between one (1) standard deviation from the mean in either side is 68.27%.
The shaded area between μ - 2σ and μ + 2σ (blue colour) represents an area whose total probability is 95.45%. This means that the probability of the occurence of an event (or observation) whose value is between two (2) standard deviations from the mean in either side is 95.45%.
The shaded area between μ - 3σ and μ + 3σ (green colour) represents an area whose total probability is 99.73%. This means that the probability of the occurence of an event (or observation) whose value is between two (3) standard deviations from the mean in either side is 99.73%.
The 68.27%, 95.45% and 99.73% are the standard confidence levels. We can use any confidence levels that we want. In finance, we generally use 95% and 99% confidence levels.
Example of using a normal distribution for calculating VaR
The following are the prices of Bank of America's common equity stock between 14th Sep 2020 and 28th Sep 2020 (11 days).| Sl No | Date | Stock Price ($) |
|---|---|---|
| 1 | 14th Sep 2020 | 25.75 |
| 2 | 15th Sep 2020 | 25.28 |
| 3 | 16th Sep 2020 | 25.60 |
| 4 | 17th Sep 2020 | 25.35 |
| 5 | 18th Sep 2020 | 25.21 |
| 6 | 21st Sep 2020 | 24.47 |
| 7 | 22nd Sep 2020 | 23.94 |
| 8 | 23rd Sep 2020 | 23.26 |
| 9 | 24th Sep 2020 | 23.34 |
| 10 | 25th Sep 2020 | 23.49 |
| 11 | 28th Sep 2020 | 24.09 |
We can use the above information to calculate the VaR of Bank of America's stock. However, to do that, first, we need to calculate the return, mean and standard deviation. The following is the calculation.
Calculating Price Returns
| Sl No | Stock Price | Change over previous | Change over previous (%) |
|---|---|---|---|
| 1 | 25.28 | 25.28 - 25.75 = -0.47 | 1.825% |
| 2 | 25.60 | 25.60 - 25.28 = +0.32 | 1.265% |
| 3 | 25.35 | 25.35 - 25.60 = -0.25 | -0.976% |
| 4 | 25.21 | 25.21 - 25.35 = -0.14 | -0.552% |
| 5 | 24.47 | 24.47 - 25.21 = -0.74 | -2.935% |
| 6 | 23.94 | 23.94 - 24.47 = -0.53 | -2.165% |
| 7 | 23.26 | 23.26 - 23.94 = -0.68 | -2.840% |
| 8 | 23.34 | 23.34 - 23.26 = +0.08 | 0.343% |
| 9 | 23.49 | 23.49 - 23.34 = +0.15 | 0.642% |
| 10 | 24.09 | 24.09 - 23.49 = +0.6 | 2.554% |
The arithmetic mean of the stock price returns is:
\[ Mean = {\sum X \over N } = {-2.839 \text % \over 10} = -0.2839 \text % \]
| Sl No | Return (X) | Mean (X̄) | Deviation x = (X- X̄) | Deviation x2 |
|---|---|---|---|---|
| 1 | 1.825% | -0.2839 | 2.1089 | 4.4474 |
| 2 | 1.265% | -0.2839 | 1.5489 | 2.3990 |
| 3 | -0.976% | -0.2839 | -0.6921 | 0.4790 |
| 4 | -0.552% | -0.2839 | -0.2681 | 0.0718 |
| 5 | -2.935% | -0.2839 | -2.6511 | 7.0283 |
| 6 | -2.165% | -0.2839 | -1.881 | 3.5381 |
| 7 | -2.840% | -0.2839 | -2.556 | 6.5331 |
| 8 | 0.343% | -0.2839 | 0.6269 | 0.3930 |
| 9 | 0.642% | -0.2839 | 0.9259 | 0.8572 |
| 10 | 2.554% | -0.2839 | 2.8379 | 8.0536 |
The standard deviation of the stock price returns is:
\[ Standard \; Deviation = \sqrt {\sum x^2 \over N } \; = \sqrt {33.8005 \over 10} \; = \sqrt {3.38005} \; = 1.8384 \text % \]